Перегляд простору станів
Пошук у просторі станів є основою багатьох методів штучного інтелекту, він використовується, наприклад, для вирішення логічних завдань, вибору оптимального ходу, пошуку найкоротшого шляху або планування дій робота.
Простір станів завдання складається зі станів (можливих конфігурацій завдання) і дій (переходів між станами). Один із станів є початковим і принаймні один стан є цільовим. Переходи можуть мати пов’язану ціну.
Простір станів як граф
Простір станів можна представити значним орієнтованим графом, вершини якого відповідають станам, а ребра — діям. Граф простору станів занадто великий для більшості практичних завдань, щоб побудувати його повністю у пам’яті, але деякі алгоритми пошуку поступово створюють частину цього графа.
План – це будь-яка послідовність дій. Рішення завдання – це такий план, який переводить нас із початкового стану до цільового. Оптимальне рішення – це рішення, яке має найменшу вартість. (Ціна плану найчастіше є сумою цін окремих переходів.)
Приклад простору станів (ельф на сітці)
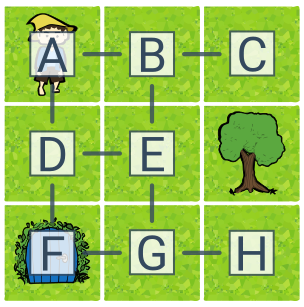
Завдання – завести ельфа у будинок. Простір станів завдання має 8 станів (A–H) і 4 дії (вліво, вправо, вниз, вгору). Початковий стан — А, цільовий — F. Оптимальним рішенням завдання є, наприклад, план вниз—вниз. Прикладом рішення, яке не є оптимальним, є праворуч—вниз—ліворуч.
Спроба всіх варіантів
Найпростішим алгоритмом, який завжди знаходить рішення (якщо воно існує), є згенерувати та перевірити. Цей алгоритм генерує всі можливі плани та перевіряє, чи є вони вирішенням проблеми. Отже, це використання грубої сили — методу розробки алгоритму, заснованого на спробі всіх можливостей. Основним недоліком грубої сили є її трудомісткість. Кількість можливих планів експоненціально зростає з довжиною плану.
Скільки існує різних планів?
Якщо у нас 4 різні дії (P – вправо, D – вниз, L – вліво, H – вгору), то є 4 плани довжини 1, але вже 4^2 плани довжини 2 (PP, PD, PL, PH, DP, DD, DL, DH, LP, LD, LL, LH, HP, HD, HL, HH), плани 4^3 довжиною 3, плани 4^4 довжиною 4 тощо.
Загалом існує k^n планів довжини n з k діями. Наприклад, для 3 можливих дій є 3^5 = 243 планів з 5 кроків, утричі більше планів з 6 кроків, 3^6 = 729, а плани з 20 кроків становлять 3^{20 }, що становить кілька мільярдів.
Дерево пошуку
Однак багато планів можуть бути взагалі нездійсненними, або вони неодноразово повертаються до того самого стану. Тому більш вигідно безперервно тестувати плани після кожної дії – як тільки ми досягаємо тупикової ситуації або раніше дослідженого стану, нам не потрібно досліджувати будь-які інші плани, починаючи з цієї послідовності дій.
Дерево пошуку – це загальна назва такого способу пошуку, коли ми поступово будуємо та оцінюємо плани після кожної дії. Процедуру пошуку плану можна описати за допомогою дерева пошуку, в якому вершини представляють плани (і водночас стан, до якого ми приходимо, виконуючи план), а орієнтовані ребра представляють дії, які розширюють попередній план на один крок. Дерево пошуку фіксує простір станів у міру його поступового виявлення алгоритмом пошуку. Існує кілька варіантів пошуку дерева, які відрізняються планом розширення (тобто який із виявлених станів досліджується наступним).
Пошук у глибину (DFS, англ. Depth First Search) вибирає останній виявлений стан. DFS має добру пам’ять, оскільки запам’ятовує лише плани поточної гілки дерева пошуку.
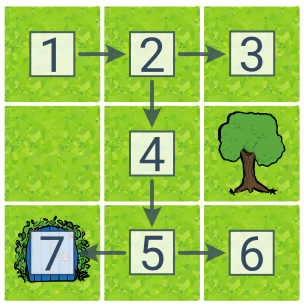
У цьому прикладі ми припускаємо, що DFS намагається виконувати дії за годинниковою стрілкою (праворуч–вниз–ліворуч–вгору). Цифри біля статусів описують порядок появи. Мета була знайдена на кроці 7, а знайдений план складається з 4 кроків (вправо–вниз–вниз–ліворуч).
Пошук у ширину (BFS, англ. Breadth First Search) шукає стани шар за шаром відповідно до кількості дій із початкового стану. Хоча це збільшує складність пам’яті (потрібно запам’ятати більше станів), це краще приводить до найкоротшого рішення.
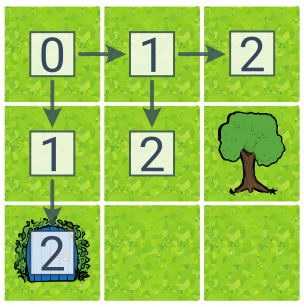
Числа для станів у зразку BFS являють собою відстані від початкового стану, що відповідає порядку обходу «шар за шаром». BFS знайшов оптимальне рішення (вниз–вниз) після дослідження 6 станів.
Uniform Cost Search (UCS, англ. Uniform Cost Search) — це варіант BFS, який дозволяє знайти найдешевше рішення, навіть якщо дії мають різні ціни. Ми вибираємо план із найнижчою ціною для розширення.
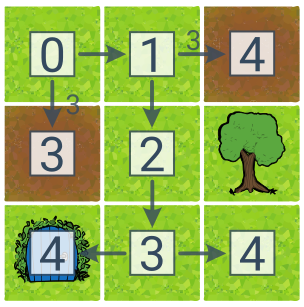
Для демонстрації UCS ми додали два коричневих болота з утричі більшою вартістю переходів на карту. Цифри у квадратах тут відображають вартість плану. У цьому випадку найдешевшим рішенням (з вартістю 4) є праворуч–вниз–вниз–ліворуч, і UCS знаходить його. (BFS поверне рішення вниз–вниз із вартістю 6).
Алгоритм дерева пошуку
Під час використання дерева пошуку ми підтримуємо набір станів, які хочемо дослідити у майбутньому, так званий край. На кожному кроці ми видаляємо один стан із краю та розміщуємо його наступників на краю (тобто стани, які можна досягти з видаленого стану однією дією). Загальна схема пошуку дерева така:
- Поставте початковий стан на край.
- Повторюйте наступні дії, доки не знайдете ціль.
- Видаліть один стан з краю. Якщо це ціль, закінчуйте пошук.
- В іншому випадку розгорніть край, тобто включіть у рішення його наступників.
- Якщо край порожній, шляху до пункту призначення немає.
Згадані варіанти дерева пошуку відрізняються тим, яку стратегію вони використовують для вибору стану з краю (крок 3), тобто як вони реалізують край. Пошук у глибину (DFS) використовує стек (ми беремо останній вставлений стан), пошук у ширину (BFS) — чергу (ми беремо найраніший вставлений стан), а пошук на основі вартості (UCS) — пріоритетну чергу (ми беремо стан із найнижчою ціною найдешевшого плану, що веде до цього стану).
Крім того, щоб уникнути повторного дослідження тих самих станів, ми можемо зберегти набір уже досліджених станів і не розширювати їх знову. Це розширення іноді називають загальним пошуком на графі, щоб відрізнити його від пошуку по дереву без перевірки раніше досліджених станів. Недоліком є збільшення вимог до пам’яті.
Інформований пошук
Пошук можна пришвидшити за допомогою евристики, яка забезпечує оцінку відстані до цілі. Така інформація стосується конкретного завдання. Ми називаємо пошук за допомогою евристики інформованим пошуком. (На відміну від цього ми називаємо алгоритми у попередніх розділах «неінформованими»).
Голодний пошук дотримується лише значення евристики та завжди вибирає дію, яка наближає нас до мети. Якщо є ризик тупикових ситуацій, необхідно поєднати голодний підхід з деревом пошуку (так зване голодне дерево пошуку) – наступним станом вибираємо той, у якого за евристикою найнижча цінова оцінка. Голодний пошук дуже швидкий, але не гарантує знаходження оптимального рішення.
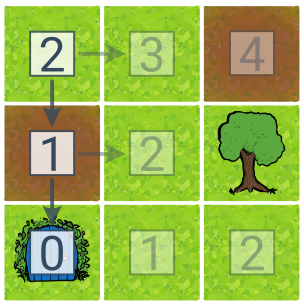
У цьому прикладі голодного дерева пошуку числа для станів відповідають евристичній оцінці вартості до місця призначення. Евристика — це відстань від цілі, яка розраховується як сума відхилень стовпців і рядків. Алгоритм знайшов шлях до місця призначення за два кроки, але це не найдешевший маршрут.
A* пошук („A star“) поєднує пошук на основі вартості (UCS) з евристикою. Це пошук по дереву, де в ролі наступного стану ми обираємо стан, який має найменшу суму ціни на даний момент і евристичну оцінку ціни, що залишилася до цілі. Якщо евристика оптимістична (забезпечує нижчу оцінку справжньої ціни), тоді A* досягне оптимального рішення і знайде його тим швидше, чим ближче евристика надає оцінки справжньої ціни.
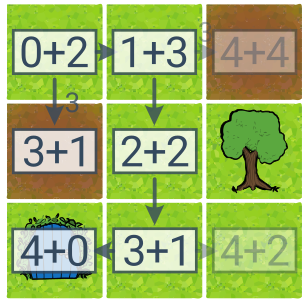
Сума станів описує пріоритет для A*: [поточна ціна] + [орієнтовна ціна, що залишилася]. A* знайшов оптимальне рішення, досліджуючи менше штатів, ніж UCS (6 замість 8).
Вибір
Швидке практикування шляхом вибору з двох варіантів.





