Регресія (у контексті машинного навчання) — це завдання оцінки числового значення якоїсь величини залежно від одного або кількох атрибутів (наприклад, оцінка ціни квартири на основі її площі). Лінійна регресія – це розв’язання задачі регресії за допомогою лінійної моделі, тобто моделі, яка є лінійною функцією (тобто зваженою сумою) оптимізованих параметрів.

Найпростішим прикладом лінійної регресії є пошук лінії \hat{y} = ax + b, яка найкраще описує зв’язок між x і y координатами вказаних точок D = \{(x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\}. У наведеному вище випадку x – площа, y – фактична ціна квартири, а \hat{y} – оцінка ціни відповідно до моделі. Модель має два параметри (a, b), які необхідно визначити (навчання моделі, оптимізація).

Квадратична похибка

Для того щоб вибрати «найкращу» лінію, нам потрібно встановити функцію помилок, яка описує, наскільки дана лінія відповідає заданим точкам. Найчастіше використовується квадратична похибка, яка визначається як сума квадратів відхилень індивідуальних оцінок від реальності. Цей підхід називають методом найменших квадратів, оскільки ми мінімізуємо суму квадратів. Помилка залежить від параметрів a, b і набору точок D:

E(a, b, D) = \sum_{(x,y) \in D} (\hat{y} - y)^2 = \sum_{(x,y) \in D} (ax + b - y)^2

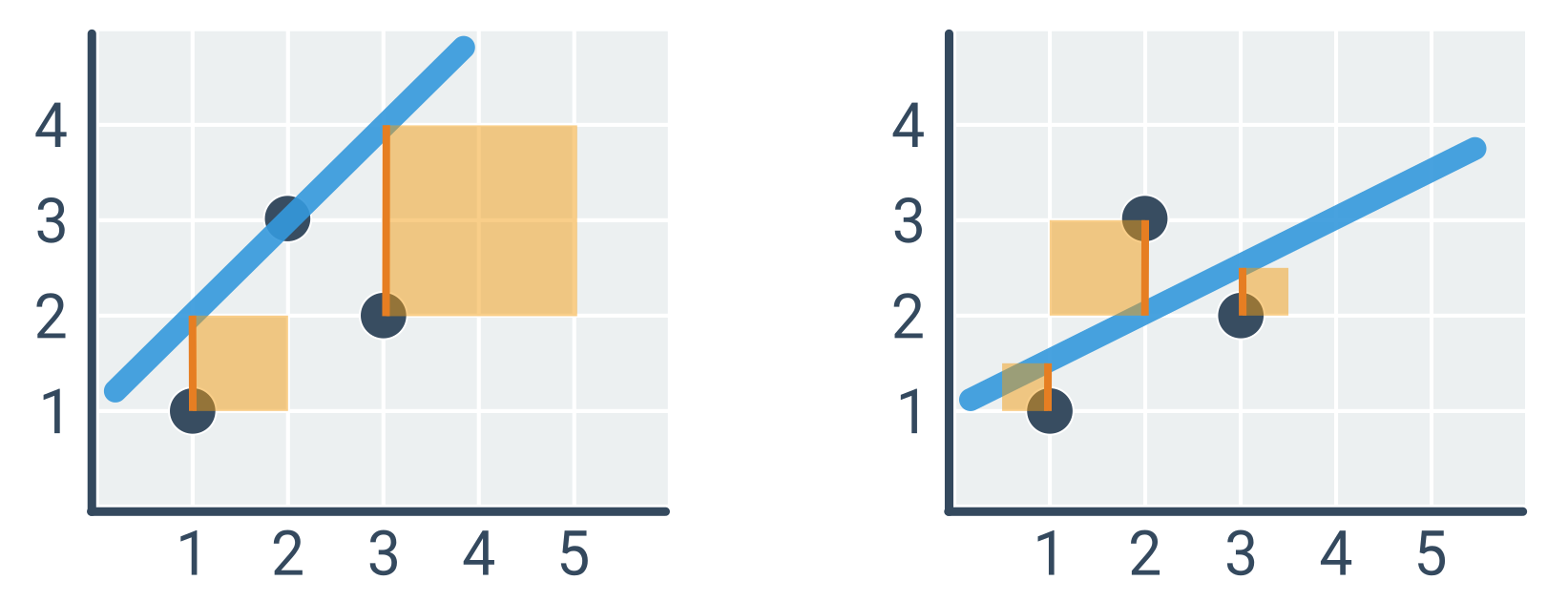
Рядок ліворуч (\hat{y} = x + 1) має квадратичну похибку 1^2 + 2^2 = 5, а рядок праворуч (\hat{y} = 0{ ,}5x + 1) лише 0{,}5^2 + 1^2 + 0{,}5^2 = 1{,}5.

Квадратична помилка чутлива до викидів, тобто точок, які лежать далеко від інших, через потужність відхилень. Іноді викиди просто видаляються. У будь-якому випадку про них краще знати.

Оптимізація параметрів

Завдання полягає в тому, щоб знайти такі значення параметрів a, b, які мінімізують квадратичну похибку. Існує ряд загальних підходів до оптимізації, таких як систематичне тестування різних комбінацій значень параметрів (груба сила) або поступове вдосконалення однієї комбінації параметрів з незначними коригуваннями (градієнтний спуск). Однак у випадку лінійної регресії оптимальні параметри можна визначити аналітично, тобто прямим розрахунком за такими формулами:

a = \frac{\sum (x - \bar{x})(y - \bar{y})}{\sum (x - \bar{x})^2}

b = \bar{y} - a\bar{x}

Суми \sum означають суму по всіх точках (x, y) \in D. \bar{x}, \bar{y} — середні значення x і y. Таким чином, чим вище напрямок a, тим сильніший зв’язок між x і y і чим більші відхилення y відносно відхилень x. Ми отримуємо рівняння для b з інтуїтивно зрозумілого співвідношення між середніми значеннями: \bar{y} = a\bar{x} + b. (Формулу можна отримати через похідну функції квадратичної похибки, яка має бути принаймні рівною 0.)

Загальна лінійна регресія

Зазвичай існує більше атрибутів, на основі яких ми робимо оцінки. Тоді лінійна модель має параметр для кожного атрибута. Наприклад, ми хочемо оцінити швидкість тварини на основі її ваги та довжини кінцівок:

\hat{y} = w_0 + w_1 x_1 + w_2 x_2

\hat{y} — оцінка швидкості, x_1 — вага, x_2 — довжина кінцівки, а w_i — параметри моделі, яку ми вивчаємо (як a, b у випадку моделі з одним атрибутом). Існує формула для розрахунку оптимальних параметрів, яка є узагальненням наведених вище формул для прямої.

Лінійна модель також може мати елементи для нелінійних перетворень атрибутів. Наприклад, щоб оцінити швидкість тварини, ми можемо використати квадрат її ваги: ​​\hat{y} = w_0 + w_1 x_1 + w_2 x_2 + w_3 x_1^2. Важливо, що функція є лінійною щодо параметрів w_i, оскільки інші значення є конкретними числами, отриманими з атрибутів прикладу.

Лінійні моделі добре інтерпретуються. Чим вище абсолютне значення параметра, тим більший вплив пов’язаного атрибута на оцінене значення. Якщо параметр додатний, то оцінене значення зростає зі збільшенням значення атрибута, а якщо параметр від’ємний, то оцінене значення зменшується зі збільшенням значення атрибута.