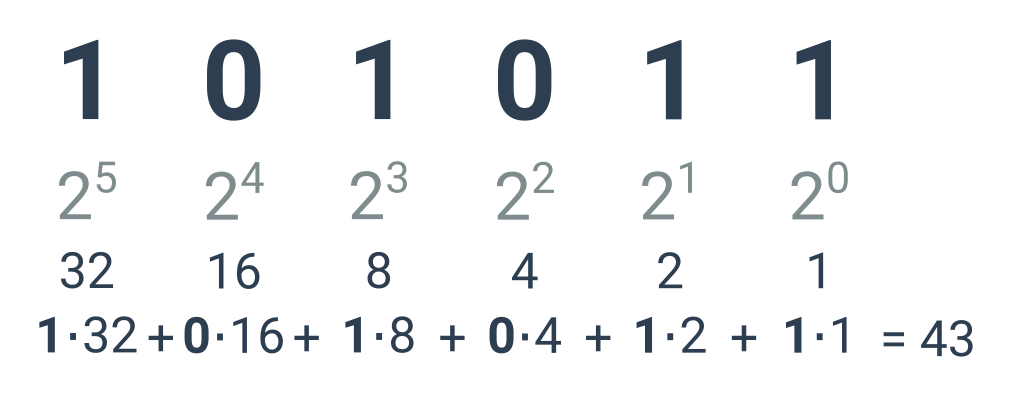Двійкові числа: основи

Принцип двійкової системи
У двійковій системі ми записуємо числа, використовуючи тільки дві цифри: 0 і 1. Положення кожної цифри в записі відповідає певному степеню двійки. Степені завжди починаються з нульового ступеня крайньої правої цифри і зростають ліворуч. Потім ми обчислюємо значення двійкового числа як суму цих степенів. Ми враховуємо кожен ступінь, якщо у відповідній позиції є 1, або не враховуємо, якщо в даній позиції є 0.
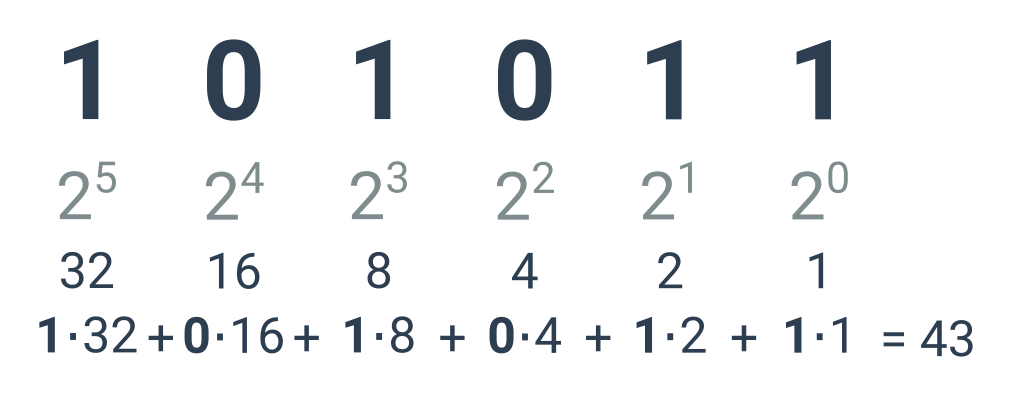
Маркування систем
Щоб розрізнити, чи йде мова про число у двійковій чи десятковій системі, ми додаємо нижні індекси до чисел, що позначають систему. Наприклад, число 5 у десятковій системі буде записано як 5_{10}, двійкове число зі значенням 5 буде записано як 101_2. Тоді ми можемо чітко визначити, що, наприклад, під нотацією 11_{10} ми маємо на увазі десяткове число 11, тоді як нотація 11_2 буде інтерпретуватися як двійкове число 11 і, отже, як десяткове число 3.
Інтуїтивна підказка
Щоб отримати базове уявлення про двійкові числа, ми можемо використовувати інструмент, який у нас завжди під рукою, а саме саму руку. Уявімо, що ми пишемо на пальцях степені двійки:
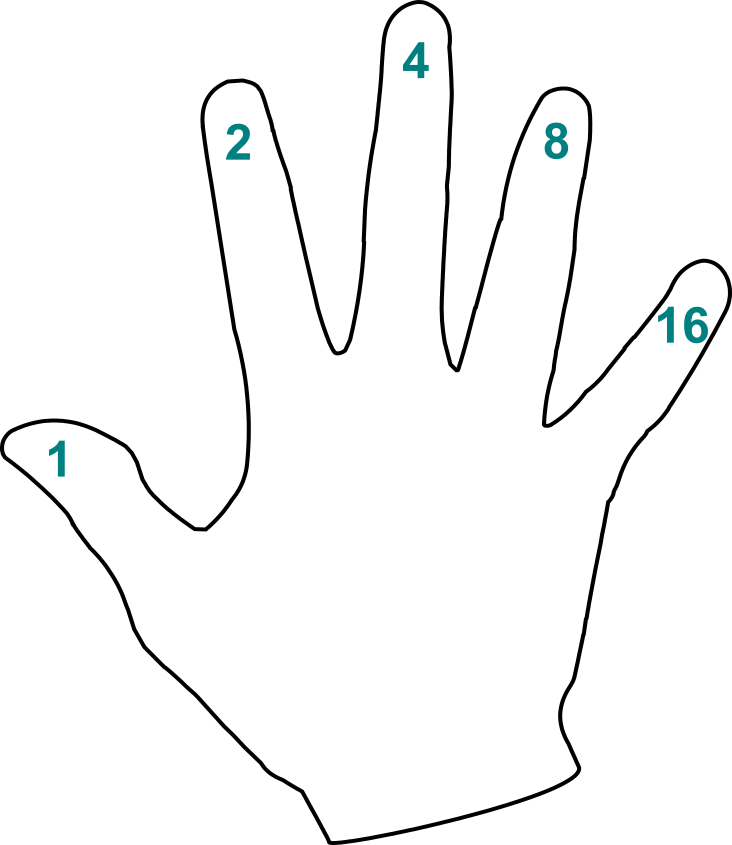
Тоді ми можемо рахувати на пальцях однієї руки не тільки до п’яти, але й до тридцяти одного. Кожне число можна виразити (однозначно) як суму степенів двійки. Якщо позначити положення пальців нулями й одиницями, то отримаємо запис у двійковій системі.
Приклади
| 1 |
1 |
1 |
| 2 |
2 |
10 |
| 3 |
2+1 |
11 |
| 4 |
4 |
100 |
| 5 |
4+1 |
101 |
| 6 |
4+2 |
110 |
| 7 |
4+2+1 |
111 |
| 8 |
8 |
1000 |
| 9 |
8+1 |
1001 |
| 10 |
8+2 |
1010 |
| 16 |
16 |
10 000 |
| 20 |
16+4 |
10 100 |
| 30 |
16+8+4+2 |
11 110 |
Закрити