Рекурсія

Рекурсія це використання самого себе. Прикладом є використання терміна у власному визначенні або зображення, що містить його зменшену копію. Рекурсивна функція – це функція, яка використовує саму себе (з різними значеннями параметрів) для обчислення. Використання рекурсії часто приводить до елегантного вирішення проблеми. Деякі мови програмування використовують рекурсію як основний засіб повторення операторів (замість циклів).

Факторіал – приклад рекурсивного визначення

Факторіал числа n (позначається як n!) є добутком чисел 1 \cdot 2 \cdot 3 \cdot \ldots \cdot n. Наприклад, 4! = 1 \cdot 2 \cdot 3 \cdot 4 = 24.. Факторіал можна визначити рекурсивно:

0! = 1

n! = n \cdot (n - 1)! \text{ для } n > 0

Це не визначення в колі, тому що при застосуванні визначення відбувається спрощення (факторіал n визначається факторіалом n - 1), а базовий випадок (n = 0) без рекурсії також визначено, до чого все веде. Тож це, скоріше, визначення по спіралі.

Рекурсивне загвинчування лампочки

A: На скільки обертів мені потрібно прокрутити, щоб вкрутити лампочку?

B: Якщо вона вже вкручена, то 0. В іншому випадку поверніть її один раз, запитайте мене ще раз і додайте 1 до моєї відповіді.

Проєктування рекурсивних алгоритмів

Спочатку ми визначаємо підпроблеми, які нам потрібні для розв’язання нашої проблеми (так, щоб обчислити факторіал n, нам потрібно знати факторіал n - 1). Ми вирішуємо ці підзадачі рекурсивно (тобто, викликаючи функцію з різними параметрами) і збираємо отримане рішення з результатів. Крім того, необхідно визначити базовий варіант і його рішення (наприклад, факторіал 0 дорівнює 1). Базовий варіант має бути таким, щоб усі гілки обчислення досягали його з часом, інакше обчислення ніколи не завершиться.

Самопосилання

Рекурсія є прикладом більш загального явища посилання на себе, так званої самореференції. Самопосилання виникає у мові (можливо, це речення говорить саме за себе), книгах, театрі, кіно та математиці. Посилання на себе навіть є основною складовою, мабуть, найвідоміших доказів у математиці (теорема Геделя про неповноту), а також в інформатиці (існування проблем, для яких немає алгоритму для їх розв’язування, як-от: завдання визначити, чи дана програма коли-небудь зупиняється).

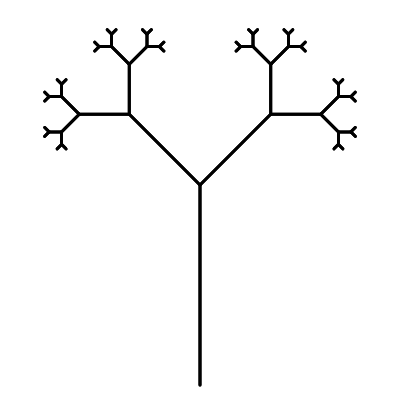
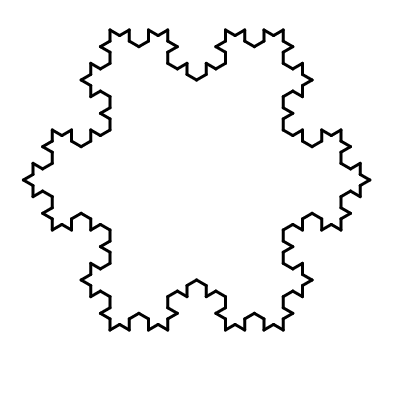
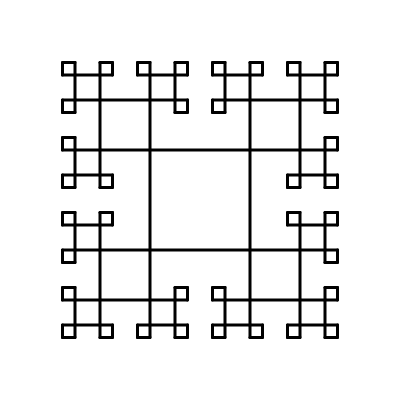
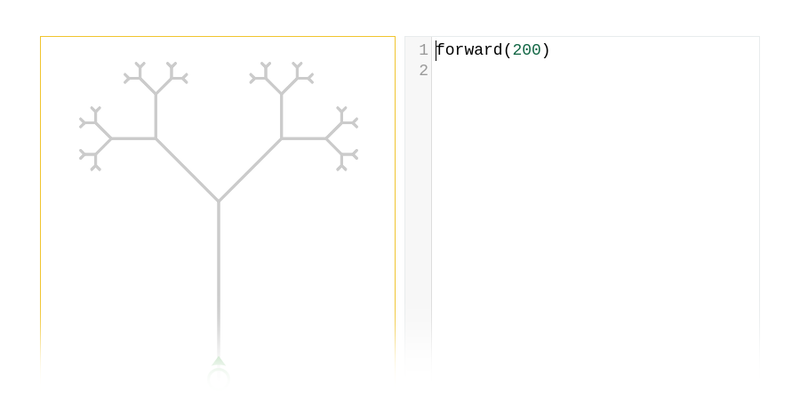
Фрактали

Поряд з рекурсією, найбільш типовим представником самопосилання є фрактали – зображення, які є самоподібними, тобто їх частини нагадують зображення в цілому. Фрактали часто можна побачити у природі (як-от, гілки дерев, папороті). Фрактали і рекурсія не є двома незалежними представниками самопосилання, між ними також існує сильний зв’язок. Рекурсія є дуже елегантним способом визначення різних фракталів. Через це ми часто можемо візуалізувати складні фрактали за допомогою простих рекурсивних функцій.